Morphology Filters

Dilation and erosion are basic operators in the area of mathematical morphology. The basic effect of dilation on an image is to gradually enlarge the boundaries of regions of foreground pixels, typically white pixels. As areas of foreground pixels grow in size, holes within those regions become smaller. The basic effect of erosion on an image is to erode away the boundaries of regions of foreground pixels, typically white pixels. As areas of foreground pixels shrink in size, holes within those areas become larger.

Dilation can also be used for edge detection by taking the dilation of an image and then subtracting away the original image, thereby highlighting just those new pixels at the edges of objects that were added by the dilation. Likewise, erosion can also be used for edge detection by taking the erosion of an image and then subtracting it away from the original image. This will highlight just those pixels at the edges of objects that were removed by the erosion. See Arithmetic Operations and Filters for information about subtracting one dataset from another.

The dilation and erosion operator takes two pieces of data as inputs — the first is the image that is to be dilated or eroded and the second is a set of coordinate points known as a structuring element or kernel. It is this structuring element that determines the precise effect of the dilation or the erosion on the input image.

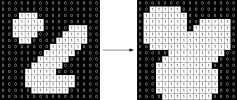
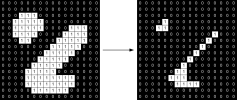
The effect of a dilation and an erosion using a 3x3 square structuring element on a binary image is shown in the following illustrations. The 3x3 square is probably the most common structuring element used in dilation and erosion operations. Larger structuring elements will produce more extreme effects. With larger structuring elements, it is quite common to use an approximately round-shaped structuring element, as opposed to a square one.

Effect of dilation on a binary image

Effect of erosion on a binary image

References

http://homepages.inf.ed.ac.uk/rbf/HIPR2/dilate.htm#1
http://homepages.inf.ed.ac.uk/rbf/HIPR2/erode.htm#1

Opening is derived from the fundamental morphological operations of erosion and dilation. The basic effect of opening is somewhat like erosion in that it tends to remove some of the foreground (bright) pixels from the edges of regions of foreground pixels. In general, it is less destructive than erosion. As with other morphological operators, the exact operation is determined by a structuring element. The effect of the operator is to preserve foreground regions that have a similar shape to the structuring element, or that can completely contain the structuring element, while eliminating all other regions of foreground pixels.

You should note that opening is the dual of closing, which means that opening the foreground pixels with a particular structuring element is equivalent to closing the background pixels with the same element.

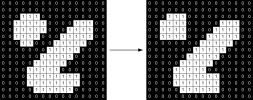
The effect of opening using a 3x3 square structuring element on a binary image is shown in the following illustration.

Effect of opening on a binary image

As with erosion and dilation, it is very common to use a 3x3 structuring element. The effect in the preceding figure is rather subtle since the structuring element is quite compact and fits into the foreground boundaries quite well even before the opening operation. Opening can also be used in conjunction with closing to achieve subtle effects.

References

http://homepages.inf.ed.ac.uk/rbf/HIPR2/open.htm#1

Closing is opening performed in reverse and can be defined simply as a dilation followed by an erosion using the same structuring element for both operations. Closing is similar in some ways to dilation in that it tends to enlarge the boundaries of foreground (bright) regions in an image and fill-in small background holes known as pepper noise. However, it is often less destructive of the original boundary shape. As with other morphological operators, the exact operation is determined by a structuring element. The effect of the operator is to preserve background regions that have a similar shape to this structuring element, or that can completely contain the structuring element, while eliminating all other regions of background pixels.

As with erosion and dilation, a 3x3 square structuring element is commonly used. The effect of closing using a 3x3 square structuring element on a binary image is shown in the following illustration.

Effect of closing on a binary image

References

http://homepages.inf.ed.ac.uk/rbf/HIPR2/close.htm

In mathematical morphology and digital image processing, top-hat transform is an operation that extracts small elements and details from given images. There are two types of top-hat transform — the white top-hat transform and the black top-hat transform. The white top-hat transform can be defined as the difference between the input image and its opening by some structuring element, while the black top-hat transform can be defined as the difference between the closing and the input image. Top-hat transforms can be used for various image processing tasks, such as feature extraction, background equalization, image enhancement, and others.

You should note that the size, or width, of the elements that are extracted by top-hat transforms can be controlled by the choice of the structuring element. The bigger the kernel, the larger the elements extracted.

References

[1] http://utam.gg.utah.edu/tomo03/03_mid/HTML/node120.html
[2] http://en.wikipedia.org/wiki/Top-hat_transform

In digital image processing, a morphological gradient is the difference between the dilation and the erosion of a given image. Applying the Morphological Gradient filter produces an image where each pixel value indicates the contrast intensity in the close neighborhood of that pixel. This can be useful for edge detection and segmentation applications.

References

[1] Morphological gradients, Jean-F Rivest, Pierre Soille, and Serge Beucher. Proc. SPIE “Image Science and Technology”, San Jose, California, Feb. 1992.